Solving "Vietnam snake" puzzle with constraint logic programming

Recently the Guardian posted a "Vietnam snake" math puzzle:

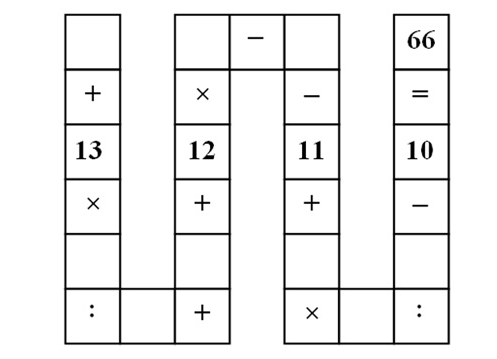
The puzzle asks to fill empty cells with integer numbers 1..9, using every number only once, such that the equality holds (order of operations: multiply and divide first, then add and subtract; colon : represents division).

Here is my program to solve the puzzle using Prolog-based ECLiPSe constraint logic programming system (https://github.com/kit1980/sdymchenko-com/blob/master/snake-puzzle-eclipse/snake.ecl):

:- lib(ic).
puzzle(A + 13 * B / C +
    D + 12 * E - F - 11 +
    G * H / I - 10 #= 66).
snake(Puzzle) :-
    term_variables(Puzzle, Vars),
    [A,B,C,D,E,F,G,H,I] = Vars,
    Vars :: 1..9,
    alldifferent(Vars),
    call(Puzzle),
    labeling(Vars).
main :-
    puzzle(Puzzle),
    findall(_, (
            snake(Puzzle),
            writeln(Puzzle)
        ), _).

The first line imports interval arithmetic constraint programming library ic. The puzzle predicate defines the linearized version of the snake puzzle from the picture.

snake constrains all variables in Puzzle to be integers in 1..9 range and pairwise different, forces the Puzzle constraint (using call), and finds a possible concrete assignment of the variables that satisfy all constraints (using labeling).

main assigns the definition of the puzzle to the Puzzle variable (it's not hard to modify this to input the puzzle definition from the user at runtime), and then uses Prolog's findall to find and print every solution.

Note that constraint programming is not just brute-force approach: clever algorithms are used behind the scenes to prune the search space.

This version assumes that every intermediate step should result in an integer (# in #= means integrality constraint on the intermediate values). After running the program we get 20 solutions:

6 + 13 * 9 / 3 + 5 + 12 * 2 - 1 - 11 + 8 * 7 / 4 - 10 #= 66
5 + 13 * 9 / 3 + 6 + 12 * 2 - 1 - 11 + 8 * 7 / 4 - 10 #= 66
9 + 13 * 3 / 1 + 6 + 12 * 2 - 5 - 11 + 8 * 7 / 4 - 10 #= 66
6 + 13 * 3 / 1 + 9 + 12 * 2 - 5 - 11 + 8 * 7 / 4 - 10 #= 66
6 + 13 * 9 / 3 + 5 + 12 * 2 - 1 - 11 + 7 * 8 / 4 - 10 #= 66
5 + 13 * 9 / 3 + 6 + 12 * 2 - 1 - 11 + 7 * 8 / 4 - 10 #= 66
9 + 13 * 3 / 1 + 6 + 12 * 2 - 5 - 11 + 7 * 8 / 4 - 10 #= 66
6 + 13 * 3 / 1 + 9 + 12 * 2 - 5 - 11 + 7 * 8 / 4 - 10 #= 66
7 + 13 * 3 / 1 + 5 + 12 * 2 - 6 - 11 + 9 * 8 / 4 - 10 #= 66
5 + 13 * 3 / 1 + 7 + 12 * 2 - 6 - 11 + 9 * 8 / 4 - 10 #= 66
7 + 13 * 3 / 1 + 5 + 12 * 2 - 6 - 11 + 8 * 9 / 4 - 10 #= 66
5 + 13 * 3 / 1 + 7 + 12 * 2 - 6 - 11 + 8 * 9 / 4 - 10 #= 66
9 + 13 * 4 / 1 + 5 + 12 * 2 - 7 - 11 + 8 * 3 / 6 - 10 #= 66
5 + 13 * 4 / 1 + 9 + 12 * 2 - 7 - 11 + 8 * 3 / 6 - 10 #= 66
9 + 13 * 4 / 1 + 5 + 12 * 2 - 7 - 11 + 3 * 8 / 6 - 10 #= 66
5 + 13 * 4 / 1 + 9 + 12 * 2 - 7 - 11 + 3 * 8 / 6 - 10 #= 66
5 + 13 * 2 / 1 + 3 + 12 * 4 - 7 - 11 + 9 * 8 / 6 - 10 #= 66
3 + 13 * 2 / 1 + 5 + 12 * 4 - 7 - 11 + 9 * 8 / 6 - 10 #= 66
5 + 13 * 2 / 1 + 3 + 12 * 4 - 7 - 11 + 8 * 9 / 6 - 10 #= 66
3 + 13 * 2 / 1 + 5 + 12 * 4 - 7 - 11 + 8 * 9 / 6 - 10 #= 66

If we change #= to $= in the puzzle definition, intermediate steps will be no longer constrained to be integers, and we'll get 136 solutions.

To learn more about ECLiPSe and get pointers to relevant resources see eclipse-clp tag on this blog.